|
| 1 | +# 426-convert-binary-search-tree-to-sorted-doubly-linked-list |
| 2 | + |
| 3 | +## Question {#question} |
| 4 | + |
| 5 | +Convert a BST to a sorted circular doubly-linked list in-place. Think of the left and right pointers as synonymous to the previous and next pointers in a doubly-linked list. |
| 6 | + |
| 7 | +Let's take the following BST as an example, it may help you understand the problem better: |
| 8 | + |
| 9 | +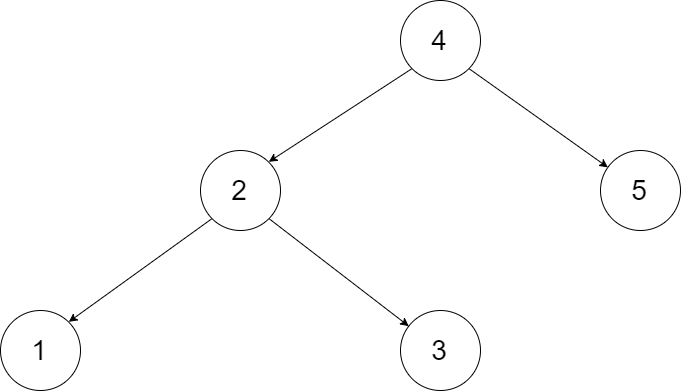 |
| 10 | + |
| 11 | +We want to transform this BST into a circular doubly linked list. Each node in a doubly linked list has a predecessor and successor. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element. |
| 12 | + |
| 13 | +The figure below shows the circular doubly linked list for the BST above. The "head" symbol means the node it points to is the smallest element of the linked list. |
| 14 | + |
| 15 | +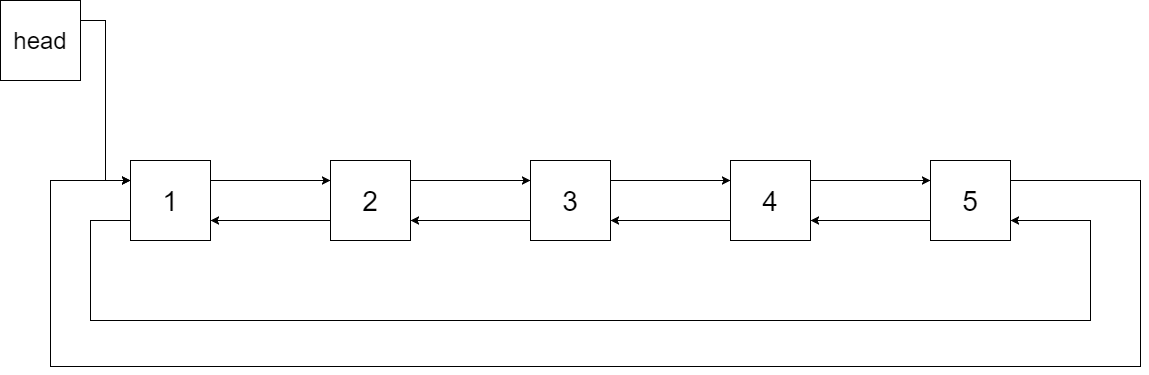 |
| 16 | + |
| 17 | +Specifically, we want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. We should return the pointer to the first element of the linked list. |
| 18 | + |
| 19 | +The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship. |
| 20 | + |
| 21 | +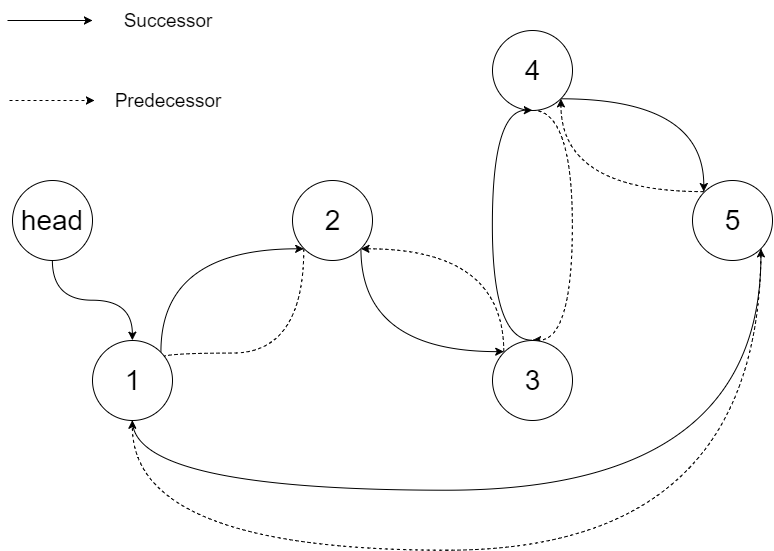 |
| 22 | + |
| 23 | + |
| 24 | + |
| 25 | +## Thought Process {#thought-process} |
| 26 | + |
| 27 | +1. Inorder traversal |
| 28 | + 1. To double link the node, we need inorder traversal to get them in the right order |
| 29 | + 2. We also need a previous node to be able to make the connection to the next node |
| 30 | + 3. To facilitate the double linking, we create a dummy node at first, which help us in returning the smallest node and also save the reference for linkage between the smallest node and largest node |
| 31 | + 4. For inorder\(root\) function, we create link as follow |
| 32 | + 1. pre.right = root |
| 33 | + 2. root.left = pre |
| 34 | + 3. pre = root \(for next linkage\) |
| 35 | + 5. At the end, we need to make sure the lastNode.right = firstNode and firstNode.left = lastNode |
| 36 | + 6. Time complexity O\(n\) |
| 37 | + 7. Space complexity O\(logn\) |
| 38 | +2. asd |
| 39 | + |
| 40 | +## Solution |
| 41 | + |
| 42 | +```java |
| 43 | +class Solution { |
| 44 | + Node pre; |
| 45 | + |
| 46 | + public Node treeToDoublyList(Node root) { |
| 47 | + // we basically need to do an in-order traversal |
| 48 | + // we find the left most node |
| 49 | + if (root == null) return null; |
| 50 | + Node dummy = new Node(0, null, null); |
| 51 | + pre = dummy; |
| 52 | + inorder(root); |
| 53 | + pre.right = dummy.right; |
| 54 | + dummy.right.left = pre; |
| 55 | + dummy.right = null; |
| 56 | + return pre.right; |
| 57 | + } |
| 58 | + |
| 59 | + private void inorder(Node cur) { |
| 60 | + if (cur == null) return; |
| 61 | + inorder(cur.left); |
| 62 | + pre.right = cur; |
| 63 | + cur.left = pre; |
| 64 | + pre = cur; |
| 65 | + inorder(cur.right); |
| 66 | + } |
| 67 | +} |
| 68 | +``` |
| 69 | + |
| 70 | +## Additional {#additional} |
| 71 | + |
0 commit comments