Graph Algorithms

Simple Graph : Graph with no self loops or multi-edges.

Incident Edges : Edges coming off a node. Degree(v) is the number of Incident Edges.

Number of Vertices: $n$ Number of Edges: $m$

Min num edges in an Unconnected Graph = 0 Min num edges in a Minimally Connnected Graph = $n - 1$

Max num edges in Simple Graph = $\frac{n \cdot (n-1)}{2}$ Max num edges in Not Simple Graph = $\infty$ because self edges are allowed.

Relationship between degree of graph and edges: $degree = 2m$

Graph Implementations

1. Edge List

   An array of pairs of vertices (Edges). If edges have weights, add either a third element to the array or more information to the object.

   The total space for an edge list is Θ(E).

   To find if the graph contains a particular edge, we have to search through the entire edge list, so O(|E|).

   Example : [[0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5]]

   Operation	Run Time
   insertVertex(K key)	$O(1)$
   removeVertex(K key)	$O(m)$
   areAdjacent(Vertex v1, Vertex v2)	$O(m)$
   incidentEdges(Vertex v)	$O(m)$

2. Adjacency Matrix

   v = Number of vertices (|V|).

   The matrix is v x v. Number of edges is irrelevant.

   An adjacency matrix can determine whether two vertices are adjacent in $O(1)$ time by looking at the corresponding entry.

   matrix[i][j] is 1 if the edge (i,j) exists in the graph, otherwise it's 0.

   The diagonal should be all 0s if the graph is Simple (no self edges).

   For an undirected graph, adjacency matrix is symmetric. For a directed graph, adjacency matrix is not necessarily symmetric.

   It takes Θ(V2) space, even if the graph is sparse.

   Example:

     [0, 1, 0, 0, 0, 0]
     [1, 0, 0, 0, 1, 0]
     [0, 0, 0, 0, 1, 0]
     [0, 0, 0, 0, 1, 1]
     [0, 1, 1, 1, 0, 1]
     [0, 0, 0, 1, 1, 0]
   

   Operation	Run Time
   insertVertex(K key)	Amortized $O(n)*$ (?)
   removeVertex(K key)	$O(n)$
   areAdjacent(Vertex v1, Vertex v2)	O(1)
   incidentEdges(Vertex v)	$O(n)$

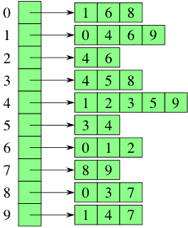
3. Adjacency List

   Combines adjacency matrices with edge lists.

   For each vertex, store an array of adjacenct vertices. Max size of array is $n - 1$.

   

   $2m$ list nodes. (?)

   Operation	Run Time
   insertVertex(K key)	O(1)
   removeVertex(K key)	O(deg(v))
   areAdjacent(Vertex v1, Vertex v2)	O( min(deg(v1), deg(v2)) )
   incidentEdges(Vertex v)	O(deg(v))

Graph BFS/DFS

Both BFS and DFS have optimal run times of $O(n + m)$.

For a DFS, just switch the Queue to a Stack.

BFS -- "CROSS" DFS -- "BACK"

void initBFS(Graoh g_) {
	// Set all vertex labels to "UNEXPLORED"
	for (auto v : g_.getVertices()) {
		g_.setVertexLabel(v, "UNEXPLORED");
	}

	// Set all edge labels to "UNEXPLORED"
	for (auto e : g_.getEdges()) {
		g_.setEdgeLabel(e, "UNEXPLORED");
	}

	// Runs BFS on all vertices
	for (auto v : g_.getVertices()) {
		if (g_.getLabel(v) == "UNEXPLORED") {
			BFS(g_, v);
		}
	}
}

void BFS(Graph g_, Vertex v) {
	Queue<Vertex> q;
	g_.setLabel(v, "EXPLORED");
	q.push(v);

	while (! q.empty()) {
		Vertex next = q.front();
		q.pop();

		for (auto adjV : g_.getAdjacentVertices(next)) {
			if (g_.getLabel(adjV) == "UNEXPLORED") {
				g_.setLabel(next, adjV, "DISCOVERY");
				q.push(adjV);
			} else g_.setLabel(next, adjV, "BACK");
		}
	}
}

Spanning Trees and Minimum Spanning Trees

Spanning Tree : Every possible vertex in G is connected with minimum number of edges. Connected and acyclic.

Minimum Spanning Tree : Spanning tree with the minimal total edge weights. Has $n-1$ edges.

Partition Property : If there's an edge of minimum weight across the partition, it's a part of the MST.

To run MST algorithm, underlying graph must be connected. So, $m \geq n + c$.

Fibionacci Heap : Decreases value of key while maintaining heap property in Amortized $O(1)$ time.

Negative weight cycles break everything.

Both Kruskal and Prim's run in $O(m log(n))$

1. Kruskal's Algorithm (MST) -- Next lowest weight edge until MST formed
   1. Choose the shortest edge
   2. Choose the next lowest weighted edge on the graph, anywhere, that wouldn't create a cycle. Do this over and over until every vertex is in the tree.

Priority Queue Implementation	Total Run Time
Heap	$O(n + m) + O(mlog(n))$
Sorted Array	$O(n + mlog(n)) + O(m)$

void KruskalMST(Graph& graph) {
	// Get a list of all edges in the graph and sort them by increasing weight.
	queue<Edge> queue;
	std::vector<Edge> edges = graph.getEdges();
	std::sort(edges.begin(), edges.end());

	for (auto edgesIter = edges.begin(); edgesIter != edges.end(); edgesIter++) {
		queue.push(*edgesIter);
	}

	// Create a disjoint sets structure where each vertex is represented by a set
	DisjointSets forest;
	std::vector<Vertex> vertices = graph.getVertices();
	int numVertices = vertices.size();
	forest.addelements(vertices.size());

	/**
	 * Traverse the list from the start (i.e., from lightest weight to heaviest).
	 * Inspect the current edge. If that edge connects two vertices from different sets,
	 	union their respective sets and mark the edge as part of the MST.
	 	Otherwise there would be a cycle, so do nothing.
	 *   Repeat this until n−1 edges have been added, where n is the number of vertices in the graph.
	 */

	int numEdgesAdded = 0;

	while (numEdgesAdded < numVertices - 1) {
		Edge nextEdge = queue.front();
		queue.pop();
		Vertex source = nextEdge.source;
		Vertex dest = nextEdge.dest;

		if (forest.find(source) != forest.find(dest)) {
			graph.setEdgeLabel(source, dest, "MST");
			forest.setunion(source, dest);
			numEdgesAdded++;
		}
	}
}

2. Prim's Algorithm (MST) -- Partition Algorithm.
   1. Choose start vertex.
   2. Add the next lowest weighted incident edge that wouldn't create a cycle and is not already visited. Do this over and over until you have an MST. https://www.youtube.com/watch?v=cplfcGZmX7I

void Prim(Graph& g, Vertex start) {

	vector<int> dist;
	vector<Vertex> predecessor;

	//Set all initial distances to max, predecessors to NULL.
	for (int i = 0; i < g.getVertices().size(); i++) {
		dist[i] = +inf ***(use 99999);
		predecessor[i] = NULL
	}

	dist[start] = 0;

	Queue<Vertex> queue;

}

Implementation	Adj. Matrix	Adj. List
Heap	$O(n^2 + mlog(n))$	$O(n log(n) + mlog(n))$
Unsorted Array	$O(n^2)$	$O(n^2)$

Shortest Path Algorithms

1. Dijkstra's Algorithm -- Closely related to Prim's

   • Can look up distance to any node in $O(1)$ time
   • Every edge needs a non-negative weight.
   • Next vertex weight is the previous vertex weight plus the edge weight to get there.
   • https://www.youtube.com/watch?v=_lHSawdgXpI
   • $O(m + nlog(n))$ when using Fibionnaci Trees (My notes say this is the same as Prim's?)

2. Floyd-Warshall

   • Similar to Dijkstra, but can be used with negative edge weights.
   • Time Complexity of $O(n^{3})$