|
| 1 | +5亿个数的大文件怎么排序? |
| 2 | +================================================== |
| 3 | +## **问题** |
| 4 | + |
| 5 | +给你1个文件`bigdata`,大小4663M,5亿个数,文件中的数据随机,一行一个整数: |
| 6 | + |
| 7 | +```bash |
| 8 | +6196302 |
| 9 | +3557681 |
| 10 | +6121580 |
| 11 | +2039345 |
| 12 | +2095006 |
| 13 | +1746773 |
| 14 | +7934312 |
| 15 | +2016371 |
| 16 | +7123302 |
| 17 | +8790171 |
| 18 | +2966901 |
| 19 | +... |
| 20 | +7005375 |
| 21 | +``` |
| 22 | + |
| 23 | +现在要对这个文件进行排序,怎么做? |
| 24 | + |
| 25 | +## 内部排序 |
| 26 | + |
| 27 | +先尝试内排,选2种排序方式: |
| 28 | + |
| 29 | +### 3路快排: |
| 30 | + |
| 31 | +```java |
| 32 | +private final int cutoff = 8; |
| 33 | + |
| 34 | +public <T> void perform(Comparable<T>[] a) { |
| 35 | + perform(a,0,a.length - 1); |
| 36 | + } |
| 37 | + |
| 38 | + private <T> int median3(Comparable<T>[] a,int x,int y,int z) { |
| 39 | + if(lessThan(a[x],a[y])) { |
| 40 | + if(lessThan(a[y],a[z])) { |
| 41 | + return y; |
| 42 | + } |
| 43 | + else if(lessThan(a[x],a[z])) { |
| 44 | + return z; |
| 45 | + }else { |
| 46 | + return x; |
| 47 | + } |
| 48 | + }else { |
| 49 | + if(lessThan(a[z],a[y])){ |
| 50 | + return y; |
| 51 | + }else if(lessThan(a[z],a[x])) { |
| 52 | + return z; |
| 53 | + }else { |
| 54 | + return x; |
| 55 | + } |
| 56 | + } |
| 57 | + } |
| 58 | + |
| 59 | + private <T> void perform(Comparable<T>[] a,int low,int high) { |
| 60 | + int n = high - low + 1; |
| 61 | + //当序列非常小,用插入排序 |
| 62 | + if(n <= cutoff) { |
| 63 | + InsertionSort insertionSort = SortFactory.createInsertionSort(); |
| 64 | + insertionSort.perform(a,low,high); |
| 65 | + //当序列中小时,使用median3 |
| 66 | + }else if(n <= 100) { |
| 67 | + int m = median3(a,low,low + (n >>> 1),high); |
| 68 | + exchange(a,m,low); |
| 69 | + //当序列比较大时,使用ninther |
| 70 | + }else { |
| 71 | + int gap = n >>> 3; |
| 72 | + int m = low + (n >>> 1); |
| 73 | + int m1 = median3(a,low,low + gap,low + (gap << 1)); |
| 74 | + int m2 = median3(a,m - gap,m,m + gap); |
| 75 | + int m3 = median3(a,high - (gap << 1),high - gap,high); |
| 76 | + int ninther = median3(a,m1,m2,m3); |
| 77 | + exchange(a,ninther,low); |
| 78 | + } |
| 79 | + |
| 80 | + if(high <= low) |
| 81 | + return; |
| 82 | + //lessThan |
| 83 | + int lt = low; |
| 84 | + //greaterThan |
| 85 | + int gt = high; |
| 86 | + //中心点 |
| 87 | + Comparable<T> pivot = a[low]; |
| 88 | + int i = low + 1; |
| 89 | + |
| 90 | + /* |
| 91 | + * 不变式: |
| 92 | + * a[low..lt-1] 小于pivot -> 前部(first) |
| 93 | + * a[lt..i-1] 等于 pivot -> 中部(middle) |
| 94 | + * a[gt+1..n-1] 大于 pivot -> 后部(final) |
| 95 | + * |
| 96 | + * a[i..gt] 待考察区域 |
| 97 | + */ |
| 98 | + |
| 99 | + while (i <= gt) { |
| 100 | + if(lessThan(a[i],pivot)) { |
| 101 | + //i-> ,lt -> |
| 102 | + exchange(a,lt++,i++); |
| 103 | + }else if(lessThan(pivot,a[i])) { |
| 104 | + exchange(a,i,gt--); |
| 105 | + }else{ |
| 106 | + i++; |
| 107 | + } |
| 108 | + } |
| 109 | + |
| 110 | + // a[low..lt-1] < v = a[lt..gt] < a[gt+1..high]. |
| 111 | + perform(a,low,lt - 1); |
| 112 | + perform(a,gt + 1,high); |
| 113 | + } |
| 114 | +``` |
| 115 | + |
| 116 | +### 归并排序: |
| 117 | + |
| 118 | +```java |
| 119 | + /** |
| 120 | + * 小于等于这个值的时候,交给插入排序 |
| 121 | + */ |
| 122 | + private final int cutoff = 8; |
| 123 | + |
| 124 | + /** |
| 125 | + * 对给定的元素序列进行排序 |
| 126 | + * |
| 127 | + * @param a 给定元素序列 |
| 128 | + */ |
| 129 | + @Override |
| 130 | + public <T> void perform(Comparable<T>[] a) { |
| 131 | + Comparable<T>[] b = a.clone(); |
| 132 | + perform(b, a, 0, a.length - 1); |
| 133 | + } |
| 134 | + |
| 135 | + private <T> void perform(Comparable<T>[] src,Comparable<T>[] dest,int low,int high) { |
| 136 | + if(low >= high) |
| 137 | + return; |
| 138 | + |
| 139 | + //小于等于cutoff的时候,交给插入排序 |
| 140 | + if(high - low <= cutoff) { |
| 141 | + SortFactory.createInsertionSort().perform(dest,low,high); |
| 142 | + return; |
| 143 | + } |
| 144 | + |
| 145 | + int mid = low + ((high - low) >>> 1); |
| 146 | + perform(dest,src,low,mid); |
| 147 | + perform(dest,src,mid + 1,high); |
| 148 | + |
| 149 | + //考虑局部有序 src[mid] <= src[mid+1] |
| 150 | + if(lessThanOrEqual(src[mid],src[mid+1])) { |
| 151 | + System.arraycopy(src,low,dest,low,high - low + 1); |
| 152 | + } |
| 153 | + |
| 154 | + //src[low .. mid] + src[mid+1 .. high] -> dest[low .. high] |
| 155 | + merge(src,dest,low,mid,high); |
| 156 | + } |
| 157 | + |
| 158 | + private <T> void merge(Comparable<T>[] src,Comparable<T>[] dest,int low,int mid,int high) { |
| 159 | + |
| 160 | + for(int i = low,v = low,w = mid + 1; i <= high; i++) { |
| 161 | + if(w > high || v <= mid && lessThanOrEqual(src[v],src[w])) { |
| 162 | + dest[i] = src[v++]; |
| 163 | + }else { |
| 164 | + dest[i] = src[w++]; |
| 165 | + } |
| 166 | + } |
| 167 | + } |
| 168 | +``` |
| 169 | + |
| 170 | +数据太多,递归太深,会导致栈溢出。数据太多,数组太长,会导致OOM。 |
| 171 | + |
| 172 | +可见这两种方式不适用。 |
| 173 | + |
| 174 | +## 位图法 |
| 175 | + |
| 176 | +BitMap算法的核心思想是用bit数组来记录0-1两种状态,然后再将具体数据映射到这个比特数组的具体位置,这个比特位设置成0表示数据不存在,设置成1表示数据存在。 |
| 177 | + |
| 178 | +BitMap算在在大量数据查询、去重等应用场景中使用的比较多,这个算法具有比较高的空间利用率。 |
| 179 | + |
| 180 | +实现代码如下: |
| 181 | + |
| 182 | +```csharp |
| 183 | +private BitSet bits; |
| 184 | + |
| 185 | +public void perform( |
| 186 | + String largeFileName, |
| 187 | + int total, |
| 188 | + String destLargeFileName, |
| 189 | + Castor<Integer> castor, |
| 190 | + int readerBufferSize, |
| 191 | + int writerBufferSize, |
| 192 | + boolean asc) throws IOException { |
| 193 | + |
| 194 | + System.out.println("BitmapSort Started."); |
| 195 | + long start = System.currentTimeMillis(); |
| 196 | + bits = new BitSet(total); |
| 197 | + InputPart<Integer> largeIn = PartFactory.createCharBufferedInputPart(largeFileName, readerBufferSize); |
| 198 | + OutputPart<Integer> largeOut = PartFactory.createCharBufferedOutputPart(destLargeFileName, writerBufferSize); |
| 199 | + largeOut.delete(); |
| 200 | + |
| 201 | + Integer data; |
| 202 | + int off = 0; |
| 203 | + try { |
| 204 | + while (true) { |
| 205 | + data = largeIn.read(); |
| 206 | + if (data == null) |
| 207 | + break; |
| 208 | + int v = data; |
| 209 | + set(v); |
| 210 | + off++; |
| 211 | + } |
| 212 | + largeIn.close(); |
| 213 | + int size = bits.size(); |
| 214 | + System.out.println(String.format("lines : %d ,bits : %d", off, size)); |
| 215 | + |
| 216 | + if(asc) { |
| 217 | + for (int i = 0; i < size; i++) { |
| 218 | + if (get(i)) { |
| 219 | + largeOut.write(i); |
| 220 | + } |
| 221 | + } |
| 222 | + }else { |
| 223 | + for (int i = size - 1; i >= 0; i--) { |
| 224 | + if (get(i)) { |
| 225 | + largeOut.write(i); |
| 226 | + } |
| 227 | + } |
| 228 | + } |
| 229 | + |
| 230 | + largeOut.close(); |
| 231 | + long stop = System.currentTimeMillis(); |
| 232 | + long elapsed = stop - start; |
| 233 | + System.out.println(String.format("BitmapSort Completed.elapsed : %dms",elapsed)); |
| 234 | + }finally { |
| 235 | + largeIn.close(); |
| 236 | + largeOut.close(); |
| 237 | + } |
| 238 | +} |
| 239 | + |
| 240 | +private void set(int i) { |
| 241 | + bits.set(i); |
| 242 | +} |
| 243 | + |
| 244 | +private boolean get(int v) { |
| 245 | + return bits.get(v); |
| 246 | +} |
| 247 | +``` |
| 248 | + |
| 249 | +## 外部排序 |
| 250 | + |
| 251 | +什么是外部排序? |
| 252 | + |
| 253 | +> 1. 内存极少的情况下,利用分治策略,利用外存保存中间结果,再用多路归并来排序; |
| 254 | +
|
| 255 | +实现原理如下: |
| 256 | + |
| 257 | +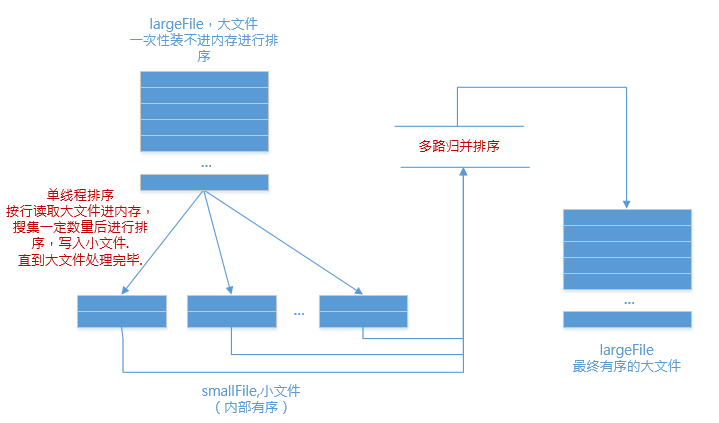 |
| 258 | + |
| 259 | +**1.分成有序的小文件** |
| 260 | + |
| 261 | +内存中维护一个极小的核心缓冲区`memBuffer`,将大文件`bigdata`按行读入,搜集到`memBuffer`满或者大文件读完时,对`memBuffer`中的数据调用内排进行排序,排序后将**有序结果**写入磁盘文件`bigdata.xxx.part.sorted`. |
| 262 | +循环利用`memBuffer`直到大文件处理完毕,得到n个有序的磁盘文件: |
| 263 | + |
| 264 | + |
| 265 | + |
| 266 | +**2.合并成1个有序的大文件** |
| 267 | + |
| 268 | +现在有了n个有序的小文件,怎么合并成1个有序的大文件? |
| 269 | + |
| 270 | +利用如下原理进行归并排序: |
| 271 | + |
| 272 | + |
| 273 | + |
| 274 | +举个简单的例子: |
| 275 | + |
| 276 | +> 文件1:**3**,6,9。 |
| 277 | +> 文件2:**2**,4,8。 |
| 278 | +> 文件3:**1**,5,7。 |
| 279 | +> |
| 280 | +> 第一回合: |
| 281 | +> 文件1的最小值:3 , 排在文件1的第1行。 |
| 282 | +> 文件2的最小值:2,排在文件2的第1行。 |
| 283 | +> 文件3的最小值:1,排在文件3的第1行。 |
| 284 | +> 那么,这3个文件中的最小值是:min(1,2,3) = 1。 |
| 285 | +> 也就是说,最终大文件的当前最小值,是文件1、2、3的当前最小值的最小值。 |
| 286 | +> 上面拿出了最小值1,写入大文件。 |
| 287 | +
|
| 288 | +> 第二回合: |
| 289 | +> 文件1的最小值:3 , 排在文件1的第1行。 |
| 290 | +> 文件2的最小值:2,排在文件2的第1行。 |
| 291 | +> 文件3的最小值:5,排在文件3的第2行。 |
| 292 | +> 那么,这3个文件中的最小值是:min(5,2,3) = 2。 |
| 293 | +> 将2写入大文件。 |
| 294 | +> |
| 295 | +> 也就是说,最小值属于哪个文件,那么就从哪个文件当中取下一行数据。(因为小文件内部有序,下一行数据代表了它当前的最小值) |
| 296 | +
|
| 297 | +感兴趣的小伙伴可以自己尝试去实现下~ |
0 commit comments